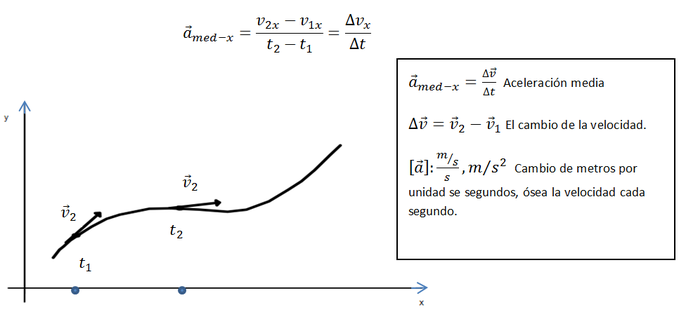
Aceleración Media.
Se define la aceleración media entre dos puntos P1 y P2 como la división de la variación de la velocidad y el tiempo transcurrido entre ambos puntos:Al igual que en la velocidad media donde se encuentra la razón de cambio para t y para x es decir Δx/Δt, la aceleración media se puede calcular de la misma manera, es decir la aceleración de una partícula donde se mueve de un punto A, aun punto B, sobre el eje x, diremos que es un vector cuya componente x es Δvx este cambio lo dividimos entre el intervalo del cambio de t es Δt, donde la expresión será: Ejemplo 1
Un automóvil parte de una posición 0m, con 0 velocidad inicial, en 6 segundos se encuentra a 10m, del punto de partida con una velocidad de 3m/s, a este llamaremos punto A, y 14 segundos después de haber salido del punto de partida se encuentra a 46m del punto de partida con una velocidad de 7m/s, a este llamaremos punto B.
a) Determine la velocidad media del punto A al punto B.
b) Determinar la aceleración media del punto A al punto B.
Identificar
En el siguiente problema necesitamos al menos dos expresiones que nos permitan encontrar los valores que necesitamos es decir velocidad media y aceleración media tenernos la información que necesitamos y a partir de ello vamos a operar.
Plantear
Es necesario seguir un orden en los procedimientos operacionales por la coherencia de los mismos, en este casos encontraremos primero la velocidad media posterior mente la aceleración media entre los dos puntos A y B.
Ejecutar
a) Para encontrar la velocidad media necesitamos realizar la siguiente operación
La velocidad media del automóvil es de 4.5 m/s, del punto A al punto B.
b) La aceleración media la podemos calcular mediante la siguiente expresión.

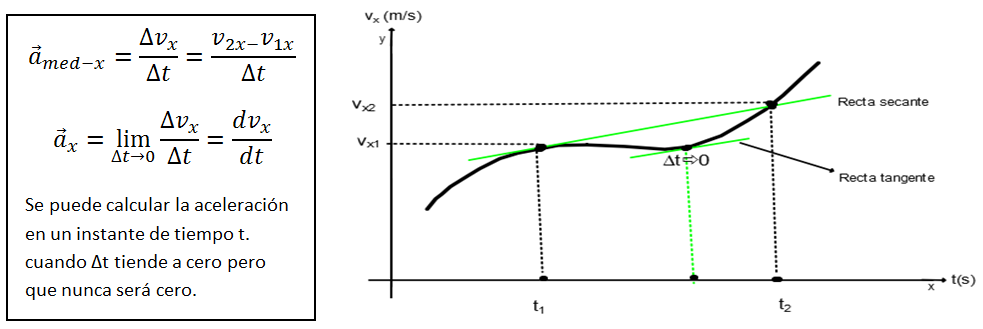
La aceleración instantánea también se puede calcular de la misma manera que la velocidad instantánea la diferencia son los valores de cambio o razones, la aceleración instantánea es el límite de la aceleración media cuando el intervalo de tiempo se acerca a cero pero que no será cero, será la derivada de vx respecto a t así dvx/dt.
La velocidad media del automóvil es de 4.5 m/s, del punto A al punto B.
b) La aceleración media la podemos calcular mediante la siguiente expresión.

Aceleración Instantánea.
La aceleración instantánea también se puede calcular de la misma manera que la velocidad instantánea la diferencia son los valores de cambio o razones, la aceleración instantánea es el límite de la aceleración media cuando el intervalo de tiempo se acerca a cero pero que no será cero, será la derivada de vx respecto a t así dvx/dt.
Se define la aceleración instantánea, o simplemente aceleración, como el límite de la aceleración media cuando el intervalo de tiempo considerado tiende a 0. También se define de manera equivalente como la derivada de la velocidad respecto al tiempo. Su expresión viene dada por:
a→=limΔt→0a→m=limΔt→0Δv→Δ t=dv→dt
donde:
a→ : Es la aceleración del cuerpo
a→m : Vector aceleración media
Δv→ : Vector variación de la velocidad
Δ t : Intervalo de tiempo que tiende a 0, es decir, un intervalo infinitamente pequeño
La aceleración es una magnitud vectorial. La ecuación de dimensiones de la aceleración instantánea es [a] = LT-2 y por tanto su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado [m/s2].
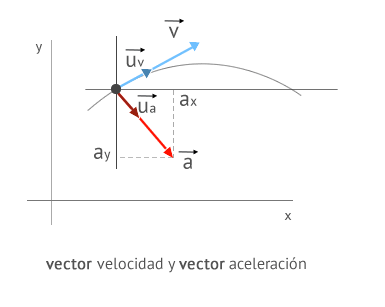
Podrás encontrar el vector aceleración escrito mediante sus componentes cartesianas quedando:
vector aceleración en 3 dimensiones coordenadas cartesianas:
a→=axi→+ayj→+azj→=(limΔt→0ΔvxΔt)i→+(limΔt→0ΔvyΔt)j→+(limΔt→0ΔvzΔt)j→=dvxdti→+dvydtj→+dvxdtj→
vector aceleración en 2 dimensiones coordenadas cartesianas:
vector aceleración en 2 dimensiones coordenadas cartesianas:
a→=axi→+ayj→=(limΔt→0ΔvxΔt)i→+(limΔt→0ΔvyΔt)j→=dvxdti→+dvydtj→
Como puedes observar, la aceleración instantánea es una magnitud vectorial que cumple:
Su módulo se puede expresar:
Mediante coordenadas cartesianas en 3 dimensiones:
∣∣a→∣∣=a2x+a2y+a2z−−−−−−−−−−√
Mediante coordenadas cartesianas en 2 dimensiones:
∣∣a→∣∣=a2x+a2y−−−−−−√
Su dirección y sentido, en general, no coincide con la del vector velocidad sino que dependen del cambio que experimente esta.
En este video podemos observar una explicación sobre aceleración media e instantánea:
Como puedes observar, la aceleración instantánea es una magnitud vectorial que cumple:
Su módulo se puede expresar:
Mediante coordenadas cartesianas en 3 dimensiones:
∣∣a→∣∣=a2x+a2y+a2z−−−−−−−−−−√
Mediante coordenadas cartesianas en 2 dimensiones:
∣∣a→∣∣=a2x+a2y−−−−−−√
Su dirección y sentido, en general, no coincide con la del vector velocidad sino que dependen del cambio que experimente esta.

En este video podemos observar una explicación sobre aceleración media e instantánea:
https://www.youtube.com/watch?v=qNVgiE_JR-A