Movimiento rectilíneo
Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.

En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil
x en el instante
t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen.
Posición
La posición
x del móvil se puede relacionar con el tiempo
t mediante una función
x=f(t).
 Desplazamiento
Desplazamiento
Supongamos ahora que en el tiempo
t, el móvil se encuentra en posición
x, más tarde, en el instante
t' el móvil se encontrará en la posición
x'. Decimos que móvil se ha desplazado
Dx=x'-x en el intervalo de tiempo
Dt=t'-t, medido desde el instante
t al instante
t'.
La velocidad media entre los instantes
t y
t' está definida por

Para determinar la velocidad en el instante
t, debemos hacer el intervalo de tiempo
Dt tan pequeño como sea posible, en el límite cuando
Dt tiende a cero.

Pero dicho límite, es la definición de derivada de
x con respecto del tiempo
t.
Para comprender mejor el concepto de velocidad media, resolvemos el siguiente ejercicio
Ejercicio
Una partícula se mueve a lo largo del eje X, de manera que su posición en cualquier instante t está dada por x=5·t2+1, donde x se expresa en metros y t en segundos.
Calcular su velocidad promedio en el intervalo de tiempo entre:
En el instante t=2 s, x=21 m
|
t’ (s)
|
x’ (m)
|
Δx=x'-x
|
Δt=t'-t
|
 m/s m/s
|
3
|
46
|
25
|
1
|
25
|
2.1
|
23.05
|
2.05
|
0.1
|
20.5
|
2.01
|
21.2005
|
0.2005
|
0.01
|
20.05
|
2.001
|
21.020005
|
0.020005
|
0.001
|
20.005
|
2.0001
|
21.00200005
|
0.00200005
|
0.0001
|
20.0005
|
...
|
...
|
...
|
...
|
...
|
|
0
|
20
|
Como podemos apreciar en la tabla, cuando el intervalo Δt→0, la velocidad media tiende a 20 m/s. La velocidad en el instante t=2 s es una velocidad media calculada en un intervalo de tiempo que tiende a cero.
Calculamos la velocidad en cualquier instante t
La posición del móvil en el instante t es x=5t2+1
La posición del móvil en el instante t+Dt es x'=5(t+Dt)2+1=5t2+10tDt+5Dt2+1
El desplazamiento es Dx=x'-x=10tDt+5Dt2
La velocidad media <v> es
La velocidad en el instante t es el límite de la velocidad media cuando el intervalo de tiempo tiende a cero
La velocidad en un instante t se puede calcular directamente, hallando la derivada de la posición x respecto del tiempo.
En el instante t=2 s, v=20 m/s
Aceleración

En general, la velocidad de un cuerpo es una función del tiempo. Supongamos que en un instante
t la velocidad del móvil es
v, y en el instante
t' la velocidad del móvil es
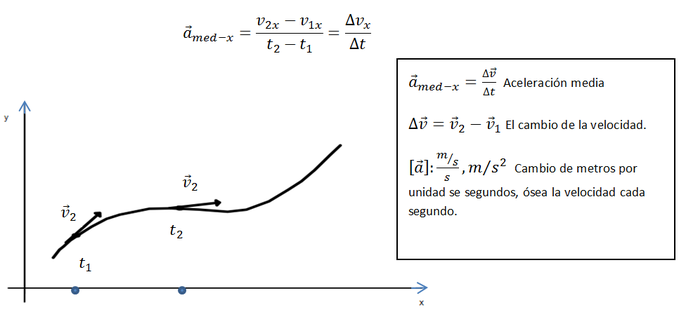
v'. Se denomina aceleración media entre los instantes
t y
t' al cociente entre el cambio de velocidad
Dv=v'-v y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio,
Dt=t'-t.

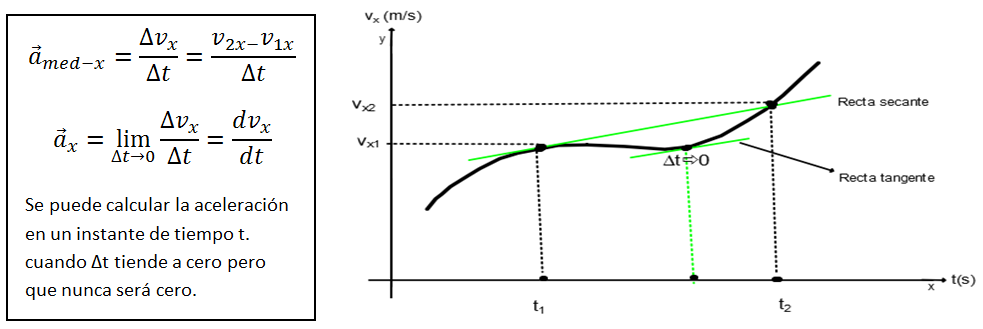
La aceleración en el instante
t es el límite de la aceleración media cuando el intervalo
Dt tiende a cero, que es la definición de la derivada de
v.
 Ejemplo
Ejemplo:
Un cuerpo se mueve a lo largo de una línea recta x=2t3-4t2+5 m. Hallar la expresión de

Si conocemos un registro de la velocidad podemos calcular el desplazamiento
x-x0 del móvil entre los instantes
t0 y
t, mediante la integral definida.

El producto
v dt representa el desplazamiento del móvil entre los instantes
t y
t+dt, o en el intervalo
dt. El desplazamiento total es la suma de los infinitos desplazamientos infinitesimales entre los instantes
t0 y
t.
 | En la figura, se muestra una gráfica de la velocidad en función del tiempo, el área en color azul mide el desplazamiento total del móvil entre los instantes t0 y t, el segmento en color azul marcado en la trayectoria recta.Hallamos la posición x del móvil en el instante t, sumando la posición inicial x0 al desplazamiento, calculado mediante la medida del área bajo la curva v-t o mediante cálculo de la integral definida en la fórmula anterior. |
Ejemplo:
Un cuerpo se mueve a lo largo de una línea recta de acuerdo a la ley v=t3-4t2 +5 m/s. Si en el instante t0=2 s. está situado en x0=4 m del origen. Calcular la posición xdel móvil en cualquier instante.

Dada la aceleración del móvil hallar el cambio de velocidad
Del mismo modo, que hemos calculado el desplazamiento del móvil entre los instantes
t0 y
t, a partir de un registro de la velocidad
v en función del tiempo
t, podemos calcular el cambio de velocidad
v-v0 que experimenta el móvil entre dichos instantes, a partir de un registro de la aceleración en función del tiempo.

 | En la figura, el cambio de velocidad v-v0 es el área bajo la curva a-t, o el valor numérico de la integral definida en la fórmula anterior.Conociendo el cambio de velocidad v-v0, y el valor inicial v0 en el instante t0, podemos calcular la velocidad v en el instante t. |
Ejemplo:
La aceleración de un cuerpo que se mueve a lo largo de una línea recta viene dada por la expresión. a=4-t2 m/s2. Sabiendo que en el instante t0=3 s, la velocidad del móvil vale v0=2 m/s. Determinar la expresión de la velocidad del móvil en cualquier instante

Resumiendo
, las fórmulas empleadas para resolver problemas de movimiento rectilíneo son

 | Un movimiento rectilíneo uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero. La posición x del móvil en el instante t lo podemos calcular integrando
o gráficamente, en la representación de v en función de t. |
Habitualmente, el instante inicial
t0 se toma como cero, por lo que las ecuaciones del movimiento uniforme resultan

Movimiento rectilíneo uniformemente acelerado
 | Un movimiento uniformemente acelerado es aquél cuya aceleración es constante. Dada la aceleración podemos obtener el cambio de velocidad v-v0 entre los instantes t0 y t, mediante integración, o gráficamente. |
 | Dada la velocidad en función del tiempo, obtenemos el desplazamiento x-x0 del móvil entre los instantes t0 y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando |
Habitualmente, el instante inicial
t0 se toma como cero, quedando las fórmulas del movimiento rectilíneo uniformemente acelerado, las siguientes.

Despejando el tiempo
t en la segunda ecuación y sustituyéndola en la tercera, relacionamos la velocidad
v con el desplazamiento
x-x0
 Video tutorial:
Video tutorial:
https://www.youtube.com/watch?v=ed1J9ZEr6fU
.jpg)